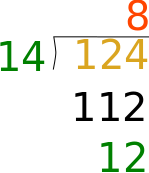Introduction to the Magic Formula
There is a formula to place increases, decreases, increase rows, buttonholes, and motifs evenly across a row (What a time saver, no more “Increase 17 stitches evenly across the row” instructions, pattern readers will love me!) But up until today I couldn’t make heads or tails of it, let alone use it.
While I’ve not been able to lay my hands on a copy of Cheryl Brunette’s Sweater 101 book, I have often borrowed Shirley Padan’s Impressive Knitwear Design Workshop from the library, which uses Brunette’s formula extensively. (My jaw drops every time I look at that sweater coat on the front cover.)
Why I could use it, but not understand it
My problem up until today is that I’m too much of a global thinker to follow sequential instructions comfortably – I’m one of those people who keeps muttering “Why are these taxes so hard – I’m good at math!”
This morning I was up to the part of editing the knitted counterpart of the Attleboro Sweater where I need to make sure I’ve calculated properly how to decrease evenly from the ribbed section to the garter stitch section, and I wanted to use the shiny new-to-me formula.
But I still didn’t understand it.
What I did to understand the Magic Formula
I printed out Ann Budd’s pdf, and pulled out the colored pencils to see if marking it up would help me understand it, because color can make patterns plain.
My husband is home this week to use up his days off, and has to write the deacon’s board report for the church’s annual meeting. Naturally, when he saw me trying to understand the math, my engineer got intrigued and asked me to explain it, while he played on a spread sheet to be sure with a set of series that he understood me. I was annoyed and wanted to keep my numbers to myself – but his exercise was quite helpful, once I sat down with my pencils, it jumped out at me.
So, here is the way you use algorithm:
Let’s use Ann Budd’s numbers and say you have to decrease 14 stitches evenly across a row of 124 stitches. You will have 8 stitches in each of the 14 groups of decreases, with 12 stitches left over. You could just put 6 in the beginning, and 6 at the end.
The row instructions could look like this: K6, (K6, k2tog) 14 times total, k6.
But we know there is a way to get those 12 stitches folded into some of the 14 decrease clusters, and who can resist a shiny new method?
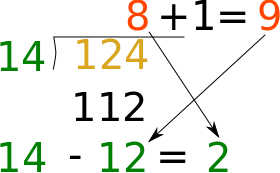
What if we took one stitch from the extra 12 stitches, and added it to a decrease cluster, so that there were 9 stitches in that cluster, and did that 12 times until they were all used up, then 12 of the clusters would have 9 stitches, and the left over clusters would still have 8 stitches in them. How many of the left over clusters? (14-12) of them.
Which is where the +1 and diagonal arrows come in. I knew they weren’t just there to look graphically cool.
The decrease row might look like this: (K6, k2tog) 2 times total, (k7, k2tog)12 times total. There, no stitches lying around extra. Except of course, you may not want to be decreasing exactly at the selvage. But if you are working a round and not a row, it’s good to go as is. If you are working a row, just write the selvage stitches in.